Mental Math – How to Teach Your Child to Multiply 2 Digits by 1 Digit under 10 Seconds

Reading Time: 6 minutes

What is Mental Math and Why It is Important

Mental math is the ability to perform calculations in one’s head. That means without the use of any external tools such as calculators, paper, or pencils. Mental math helps your child develop various cognitive skills, including memory, visualization, and the ability to manipulate numbers mentally. It helps children build a strong foundation in math – particularly by developing automaticity, the ability to quickly and accurately without exerting much mental effort. Having automaticity tremendously helps children when they solve problems involving higher-order thinking. Children who are struggling with calculation may spend a lot of time doing calculation when they encounter a difficult problem such as a multi-step word question, whereas children who have developed automaticity can use their mental capacity not on calculation but on coming up with innovative methods to solve the problem.

Teaching 2 Digits by 1 Digit Multiplication Mentally

In this blog post, we will explore a strategy that can help your child mentally perform two-digit by one-digit multiplication using decomposition. After practice, your child will potentially be able to multiply in under 10 seconds. After practicing mental math with this approach, you can demonstrate to your child how this strategy relates to the traditional “long multiplication” method done on paper.

Prerequisite

Before learning this strategy, ensure that your child can do the following:

• Accurately reciting the 9 x 9 multiplication chart and mentally performing any 1-digit by 1-digit multiplication.
• Mentally calculating the product of a multiple of 10 and a 1-digit number (e.g., 40 x 8).
• Adding up to 3-digits by 3-digits mentally (e.g., 140 + 58).

Warming Up

First, review mental math involving multiples of 10 with a single-digit number. Provide your child with some questions to help them warm up and ensure that they can perform these calculations. Remember to make this and any mental math practice enjoyable.

Example Questions:
50 x 5
10 x 4
80 x 9
40 x 7
20 x 9
50 x 1
90 x 2
70 x 8
60 x 6
30 x 5

Answers:
250
40
720
280
180
50
180
560
360
150

Introduce the Concept of Decomposition Method

Introduce the concept of the decomposition method to your child by presenting them with a question like the one below:

Mrs. Jenkins purchased a plot of empty land on which to build her new house. The length of the land is 28 meters and the width of the land is 8 meters. What is the area of the land that she bought?

Solution:

To get the total area, you have to do:

28 x 8

To do this calculation, divide the area into 20 m by 8 m and 8 m by 8 m. Show this diagram to help your child understand.

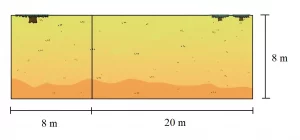
Then, ask your child to calculate each part separately and add them up. At this point, your child can do the calculation on paper.

8 x 8 = 64

20 x 8 = 160

64 + 160 = 224

So, 224 m^2 would be the area of the land, and it’s the same thing as doing 28 x 8.

Tell your child that they were able to do it by breaking down 28 into more “friendly” numbers like 20 and 8.

Give your child more similar questions involving land or any rectangular objects such as a tabletop, a room, or a soccer field. Draw a diagram similar to the above to make sure your child understands how a 2-digit number like 28 can be decomposed to more friendly numbers. Ask your child to calculate with the help of diagram and pen-and-paper.

Here’s a list of questions you might be able to use:

1. Mr. Thompson acquired a piece of vacant property to construct his dream home. The length of the property is 35 meters and the width of the property is 5 meters. What is the area of the property that he purchased? (ans: 175 m^2)
2. Brenda plans to build a fenced garden in her backyard. She wants it to be 12 meters wide and 7 meters long. What will be the total area of the fenced garden? (ans: 84 m^2)
3. Jason wants to install a tile floor in his living room and needs to determine the area of the room to know how many tiles he will need. He discovers that the room is 19 meters wide and 6 meters long. Can you help Jason calculate the area of the floor in square meter? (ans: 114 m^2)
4. Maria wants to buy a new rug for her living room. The dimensions are 25 feet by 9 feet. What is the total area of the rug Maria is planning to buy for her living room? (ans: 225 ft^2)
5. Catherine wants to create a vegetable garden in her backyard. She chose a rectangular area that is 27 meters long and 6 meters wide for her garden. What is the total area of Catherine’s vegetable garden? (ans: 162 m^2)

Shift to Mental Math using Decomposition Method

Once your child becomes comfortable with calculating the area using this method, gradually transition to the mental math method. This involves visualizing the subdivided area in their mind and breaking down the multiplication into three steps. When your child is first learning mental math, encourage them to say each step aloud.

For example, let’s say we do 46 x 7. We could say it aloud as we do it, like this:

First, I’ll break apart 46 into 40 and 6.

I have to do 40 times 7 and 6 times 7.

40 times 7 is 280.

6 times 7 is 42.

I have 280 and 42.

280 plus 42 is 322.

Saying aloud helps your child organize their thoughts and remember each step, as well as the result of each step. In the beginning, your child can also use a visual aid, such as a diagram showing subdivided areas.

As your child practices more, they will be able to rely less on saying aloud or a diagram.

Set an individual goal for each child, depending on their comfort level. Some children may be able to perform mental math in less than 10 seconds.

Here’s a list of practice questions your child can do:

Example Questions:

42 x 8
13 x 5
38 x 3
93 x 2
88 x 6
52 x 4
98 x 9
47 x 5
74 x 4
86 x 9

Answers:

336
65
114
186
528
208
882
235
296
774

How Decomposition Method Relates to Long Multiplication

Once your child becomes proficient in mental math involving the multiplication of 2-digit numbers by 1-digit numbers, you can demonstrate how this skill relates to long multiplication. Refer to the following diagram:

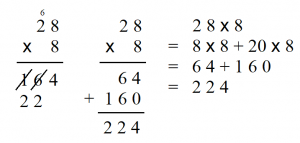
As you can see, long multiplication essentially involves decomposition on paper. When your child comprehends the reasoning behind an algebraic operation such as long multiplication, they are less likely to perceive math as merely a series of meaningless steps to follow; instead, they will understand that each step holds significance.