Mental Math – How to Teach Your Child to Multiply 3 Digits by 1 Digit under 15 Seconds

Reading Time: 5 minutes

This post is the continuation of the previous post, How to Teach Your Child to Multiply 2 Digits by 1 Digit under 10 seconds. If your child has attained the ability to multiply a 2-digit number by a 1-digit number mentally, it might be time for a new challenge: multiplying a 3-digit number by a 1-digit number.

Teaching 3 Digits by 1 Digit Multiplication Mentally

3-digit by 1-digit multiplication involves four to five mental steps and it is considered a difficult process. However, with practice, your child may be able to do it mentally, potentially under 15 seconds or less. We’ll look at how we can multiply a 3-digit number by a 1-digit number mentally by using the method of decomposition.

Prerequisite

Before learning this strategy, ensure that your child can do the following:

• Multiply a 2-digit number a 1-digit number mentally.
• Multiply a multiple of 100 by a 1-digit number (e.g. 400 x 5).
• Adding two numbers up to 10,000.

Warming Up

2-digit by 1-digit

First, have your child practice 2-digit multiplied by 1-digit mentally. An example question is 28 times 8. Break down 28 into 20 and 8, and do the following.

28 x 8

= 20 x 8 + 8 x 8

= 160 + 64

= 224

If your child is not comfortable doing this mentally, have them do it on paper, first. Slowly transition into mental math based on their comfort level. Try to encourage your child to “say it aloud”:

First, I’ll break apart 28 into 20 and 8.

I have to do 20 times 8 and 8 times 8.

20 times 8 is 160.

8 times 8 is 64.

I have 160 and 64.

160 plus 64 is 224.

Saying aloud helps your child organize their thoughts and remember the steps and the result of the steps.

Further practice questions:

32 x 6

92 x 5

72 x 4

75 x 8

22 x 3

96 x 9

51 x 7

46 x 3

85 x 6

37 x 3

Answers:

192

460

288

600

66

864

357

138

510

111

Multiple of 100 by 1-digit

Additionally, have your child complete multiplication questions between a multiple of 100 and a 1-digit number. An example is 400 x 5.

400 x 5

= 2000

(Multiply 4 with 5 to get 20. Then, make it 100 times bigger by appending two 0s to get 2000.)

Use number blocks to illustrate this if your child isn’t comfortable with this topic, yet.

 

Further practice questions:

300 x 7

800 x 2

600 x 4

900 x 3

800 x 7

600 x 6

300 x 5

100 x 9

800 x 6

700 x 7

Answers:

2100

1600

2400

2700

5600

3600

1500

900

4800

4900

Method to Multiply 3-digit by 1-digit Mentally

Now that your child is warmed up, let’s move on to multiplying 3-digit by 1-digit mentally. We’ll use the decomposition method once again. Suppose we have the following word problem:

Tony wants to measure the area of a straight road that he normally takes to go to school. He measured the width of the road to be 7 meters. From an online map, he found out that the length of the road from his home to his school is 546 meters. What is the area of the road from his home to his school?

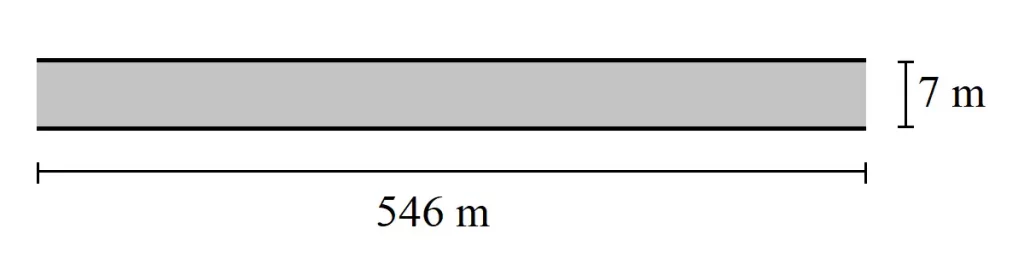
In this question, we’ll have to multiply 546 by 7.

546 x 7 = ?

We will break down 546 m into 500 m and 46 m, and calculate the two areas separately.

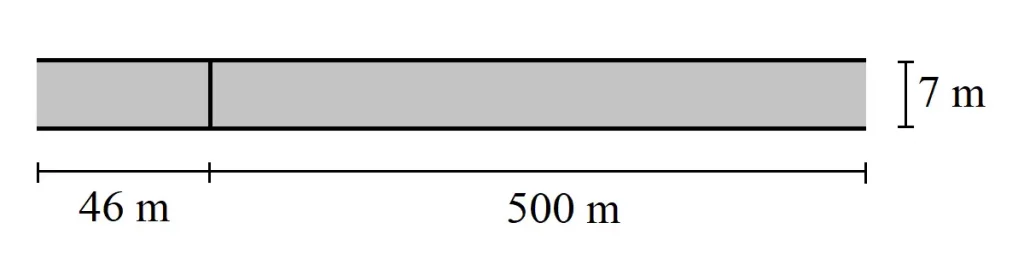
Try to have your child calculate 46 x 7, first, because this part takes more mental effort than 500 x 7. Use the mental math skill from the warm-up section, above, to calculate 46 x 7 mentally.

The answer to this part is 322 m^2.

Then, do 500 x 7 to get 3500.

Add 3500 m^2 to 322 m^2 to get 3822 m^2.

Overall, it looks like this:

546 x 7

= 46 x 7 + 500 x 7

= 322 + 500 x 7

= 322 + 3500

= 3822

“Saying aloud” may sound like this:

First, I’ll break apart 546 into 500 and 46.

I have to do 46 times 7 and 500 times 7.

First, I’ll do 46 times 7.

(46 x 7 part is omitted – it’s the same as in the warm-up section)

So, 46 times 7 is 322.

500 times 7 is 3500.

3500 plus 322 is 3822.

Notice that doing the more complex part first is advantageous because the “distance” between the answer to 46 x 7 and 3500 + 322 is only 2 steps. If you do  500 x 7 = 3500 first, then, you’ll have to do 3 to 4 more steps to get 46 x 7 = 322. By the time you add 3500 to 322, you may have forgotten 3500 from 3 steps ago.

Scaffolding is Important

Scaffolding is the process of teaching step-by-step, from simple tasks to more complex ones, from with guides and support to without. At first, your child can do the calculation on paper just to get comfortable with the whole process. Then, you can have your child try mental math while showing them a support diagram like the one shown above. You can also support your child by asking questions such as “What was the answer you got in the last step?” or giving them a hint or reminder (“You got 322 in the last step. So, what would you do now?”).

Allow your child to make progress step-by-step. Adjust the scaffold depending on your child’s progress. Remember that every child progresses at different speeds. If your child is progressing slowly, that’s okay! It might be because your child is thinking through the process in order to really understand the logic behind it.

Be Patient and Encourage Growth Mindset

Teaching mental math presents a wonderful opportunity to foster a growth mindset – the belief that intelligence is not a fixed trait one either possesses or lacks, but rather a quality that can be cultivated through dedicated effort. Any student can learn to perform mental calculations; all it requires is practice.

The amount of practice needed might vary among children, as they are all starting from different points. Practice patience with your child. Allow them to learn at their own pace and remember to give them room to make plenty of mistakes.