Mental Math – How to Teach Your Child to Multiply 2 Digits by 2 Digits under 20 Seconds

Reading Time: 6 minutes

At first glance, mentally multiplying two-digit numbers may seem challenging – and indeed it is! However, with an ample amount of practice and the right strategy, your child can master this skill. In fact, with consistent practice, they may potentially be able to complete the task in under 20 seconds. In this blog, we will explore a decomposition strategy that can enable your child to accomplish this.

Teaching 2 Digits by 2 Digits Multiplication Mentally

We will examine how to perform multiplications, such as 27 x 54, quickly through mental math. However, before we delve into that, let’s first explore the prerequisite skills.

Prerequisite

Before learning the strategy to multiply 2-digit by 2-digit, make sure that your child can do the following:

• Able to recite 9 x 9 chart flawlessly.
• Multiply a multiple of 10 by a 1-digit (e.g. 40 x 5).
• Multiply a multiple of 10 by a multiple of 10 (e.g. 30 x 80).

Warming Up

Multiple of 10 by 1-digit

First, let your child practice multiplying a multiple of 10 by a 1-digit number mentally. An example is:

40 x 5

First, do 4 x 5 to get 20. Because 40 is 10 times greater than 4, make the answer 20 ten times greater. 20 x 10 = 200. Essentially, you can add a 0 at the end of 20 to make it ten times greater.

Further practice questions:

80 x 9

20 x 7

30 x 5

60 x 5

80 x 3

70 x 7

10 x 3

60 x 4

40 x 8

50 x 2

Answers:

720

140

150

300

240

490

30

240

320

100

Multiple of 10 by Multiple of 10

Once your child knows how to multiply a multiple of 10 by a 1-digit number, it’s easy to multiply a multiple of 10 by a multiple of 10. You just have to make the answer 10 times bigger. For example, 40 x 50 is 2000. 40 x 5 is 200, so 40 x 50 is ten times greater than 200.

In other words, just add 2 zeros after the answer to 4 x 5.

Further practice questions:

80 x 90

20 x 70

30 x 50

60 x 50

80 x 30

70 x 70

10 x 30

60 x 40

40 x 80

50 x 20

Answers:

7200

1400

1500

3000

2400

4900

300

2400

3200

1000

Method to Multiply 2-digit by 2-digit

Let’s take a look at how your child can multiply 2-digit by 2-digit mentally. We’ll assume neither number is a multiple of 10. (That is, we won’t look at something like 45 x 30.)

Ana’s backyard measures 54 feet by 36 feet. She wants to know the area so she can buy the right amount of grass seeds for her backyard. Help her calculate the area of her backyard.

This question involves the following multiplication:

54 x 36

Try to have your child break down the rectangle into 4 areas, like this:

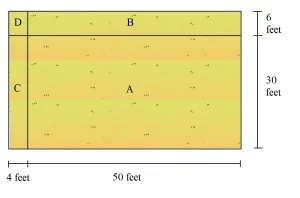
The number on each side is broken into a multiple of 10 (e.g. 50) and a 1-digit number (e.g. 4).

Ask your child to calculate the total area by adding up the areas of the subdivided areas A, B, C, and D. Your child can do the work on paper.

A: 30 x 50 = 1500

B: 6 x 50 = 300

C: 30 x 4 = 120

D: 6 x 4 = 24

Total area = 1500 + 300 + 120 + 24 = 1944

As you can see, this method breaks down the 2-digit by 2-digit multiplication into four easier multiplications and addition of the result.

Have your child do some similar multiplication problems on paper using this method until they become comfortable with the method. Here’s some questions you can use:

Q1: John’s rectangular lot measures 62 feet by 45 feet. He wants to know the area of his lot to plan his landscaping. Can you help him calculate the area of his lot?

(Answer: 2790 ft^2)

Q2: Sandy’s garden measures 45 feet by 15 feet. She wants to know the area so she can purchase the correct quantity of soil for her garden. Help her to determine the area of her garden.

(Answer: 675 ft^2)

Q3: A small table measures 74 cm by 34 cm. What is its area?

(Answer: 2516 cm^2)

Q4: In a large auditorium, students arranged chairs to prepare for a graduation ceremony. There are 67 chairs in each row, and there are 33 rows in total. How many chairs are there in total?

(Answer: 2211 chairs)

Q5: A swimming pool has 25 m length and 11 m width. What is the area that the pool occupies?

(Answer: 275 m^2)

Transition to Mental Math

Once your child is comfortable in multiplying the numbers on paper, it’s time to switch to mental math. First, make aids available to your child. For example, have your child draw a picture of the rectangle just like the one shown above, with 4 subdivided areas. Then, do the multiplication mentally while saying aloud each step.

An example question is 24 x 95. Your child may say aloud each step like this:

I have to break down 24 into 20 and 4, and 95 into 90 and 5.

I have to multiply 20 with 90, 20 with 5, 90 with 4, and 5 with 4.

20 times 90 is 1800.

20 times 5 is 100.

90 times 4 is 360.

5 times 4 is 20.

I have 1800, 100, 360, and 20.

100 plus 360 plus 20 is 460 and 20, which adds up to 480.

1800 plus 480 is 2280.

Most likely, your child would forget the results of some of the steps. In that case, jog their memory by asking a question like “What was 20 times 90 again?”, or give a hint (“You had 1800 from 20 times 90”).

As your child does more and more examples, they will become faster and faster and forget less and less. But, remember to be patient because each child progresses at different speeds.

Here are some practice questions you can give to your child:

12 x 39

74 x 28

59 x 59

93 x 54

42 x 98

16 x 75

43 x 66

25 x 29

86 x 47

33 x 62

Answers:

468

2072

3481

5022

4116

1200

2838

725

4042

2046

Connection to algebra

This method of breaking down each number into 2 parts is connected to binomial multiplication. For instance, 34 x 82 is done this way:

34 x 82

= (30 + 4) (80 + 2)

= 30 x 80 + 30 x 2 + 4 x 80 + 4 x 2

= 2400 + 60 + 320 + 8

= 2788

If a = 30, b = 4, c = 80, and d = 2, then,

(a + b) (c + d)

= ac + ad + bc + bd

For children in middle school, connection to binomial multiplication can help them understand how binomial multiplication works.